A Dirichlet process (DP) is a random probability measure $G$ over measure space $\Theta$ such that for any finite set of measurable sets $A_1,\dots,A_K$ partitioning $\Theta$ , we have

(G (A 1), \dots, G (A K)) \sim Dir (α H (A 1), \dots, α H (A K))

$(G(A_1),\dots,G(A_K )) \sim \operatorname{Dir}(\alpha H(A_1),\dots, \alpha H(A_K ))$

$H$ : Base distribution
$\alpha$ : concentration parameter

Properties (derive from the mean and variance of the Dirichlet distribution)

E (G (A i)) = H (A i)

$\operatorname{E}(G(A_i))=H(A_i)$

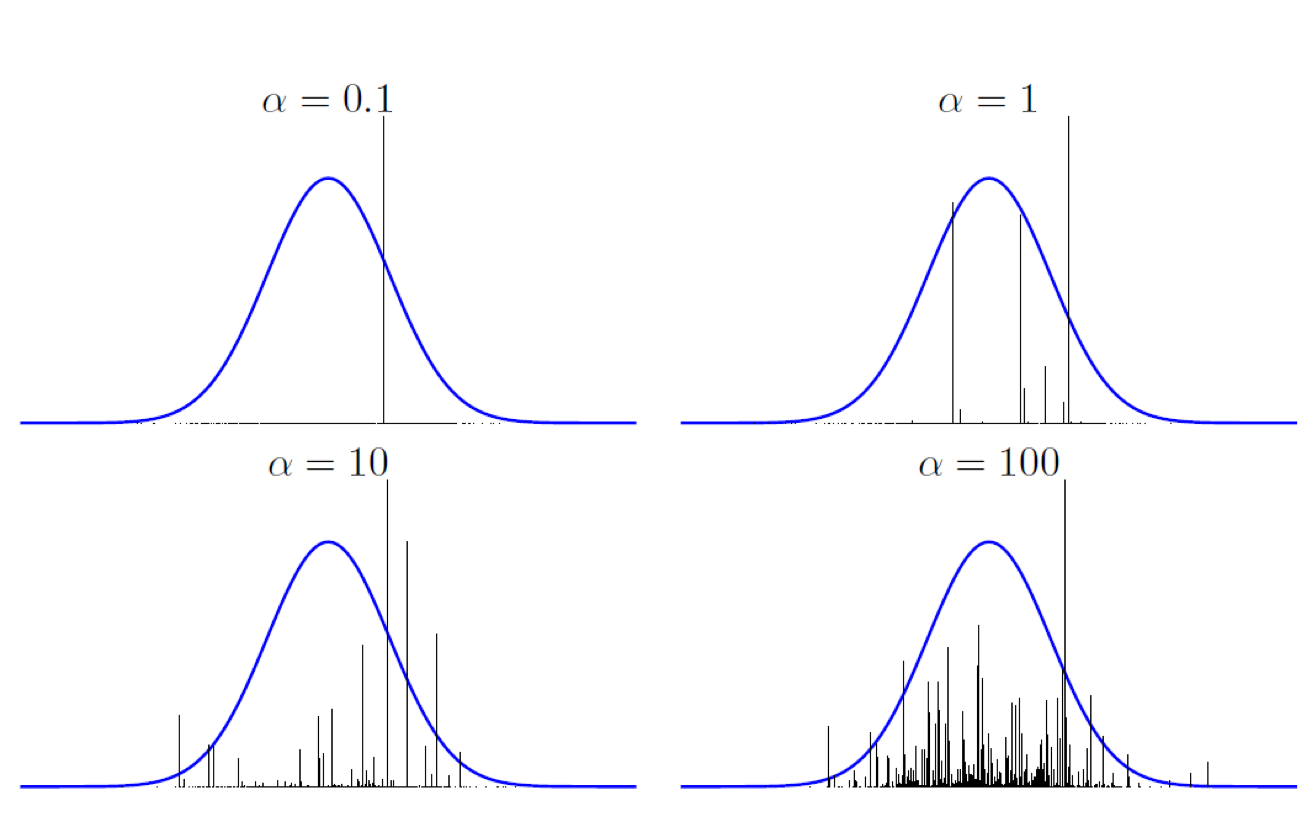
Var (G (A i)) = H ( A i ) ( 1 - H ( A i ) ) α + 1

$\operatorname{Var}(G(A_i))=\frac{H(A_i)(1-H(A_i))}{\alpha+1}$

$\alpha\to \infty$ : $\operatorname{Var}(G(A_i))\to 0$ , $G=H$ .
$\alpha\to 0$ : $\operatorname{Var}(G(A_i))\to 0$ , $\operatorname{Var}(G(A_i))\to H(A_i)(1-H(A_i))$ , similar to Bernoulli distribution.

Constructive definition: Stick-breaking constructioin

$\beta_k\sim \operatorname{Beta}(1,\alpha)$
$\theta_k\sim H$
$\pi_k=\beta_k\prod_{l=1}^{k-1}(1-\beta_l)$
$G=\sum_{k=1}^\infty\pi_k\delta_{\theta_k}$

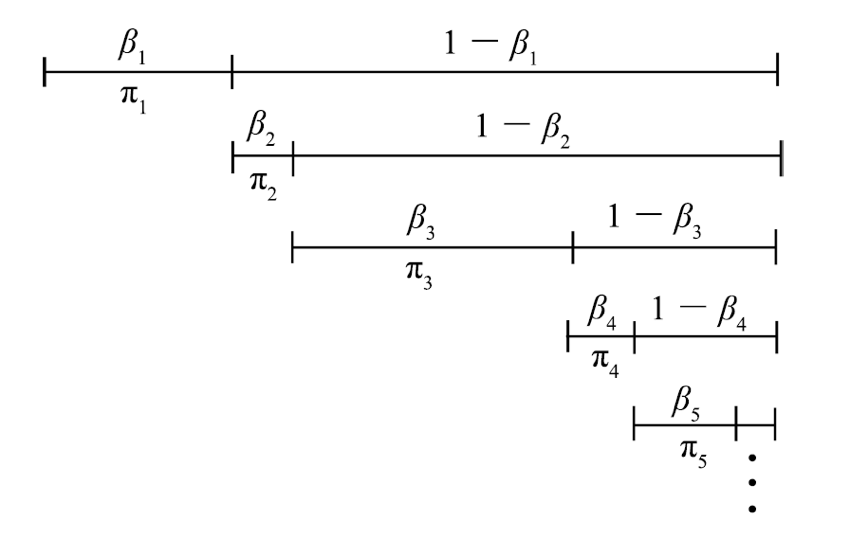
The result stick-breaking sampling has the property:

(\sum A 1 π l 1, \dots, \sum A K π l K) \sim Dir (α H (A 1), \dots, α H (A K))

$(\sum_{A_1}\pi_{l_1},\dots,\sum_{A_K}\pi_{l_K}) \sim \operatorname{Dir}(\alpha H(A_1),\dots, \alpha H(A_K ))$

Examples of different

α $\alpha$ :

Posterior:

G | θ 1, θ 2, \dots, θ n \sim DP (α + n, α H + \sum n i = 1 δ θ i α + n)

$G|\theta_1,\theta_2,\dots,\theta_n\sim \operatorname{DP}\left( \alpha+n,\frac{\alpha H+\sum_{i=1}^n \delta_{\theta_i}}{\alpha +n} \right)$
Prediction/Drawing samples:

P (θ n + 1 | θ 1, θ 2, \dots, θ n) = E (G | θ 1, θ 2, \dots, θ n) = α α + n H + \sum n i = 1 δ θ i α + n

$\begin{align} P(\theta_{n+1}|\theta_1,\theta_2,\dots,\theta_n) &{}=\operatorname E(G|\theta_1,\theta_2,\dots,\theta_n)\\ &{}=\frac{\alpha}{\alpha+n}H+\frac{\sum_{i=1}^n \delta_{\theta_i}}{\alpha+n} \end{align}$
The prediction can be seen as a Chinese Restaurant Process:
At any positive-integer time

n $n$ , the value of the process is a partition

Bn $B_n$ of the set {1, 2, 3, ... , n}, whose probability distribution is determined as follows. At time

n=1 $n = 1$ , the trivial partition { {1} } is obtained with probability 1. At time n + 1 the element n + 1 is either:

added to one of the blocks of the partition $B_n$ , where each block is chosen with probability $|b|/(n + 1)$ where $|b|$ is the size of the block (i.e. number of elements), or
added to the partition $B_n$ as a new singleton block, with probability $1/(n + 1)$ .

Reference

Nonparametric Baysian Models: http://videolectures.net/mlss09uk_teh_nbm/
Chinese restaurant process: https://en.wikipedia.org/wiki/Chinese_restaurant_process

Dirichlet Process

Reference